1.15~16 지반해석법-수치해석법
■ 수치해석법
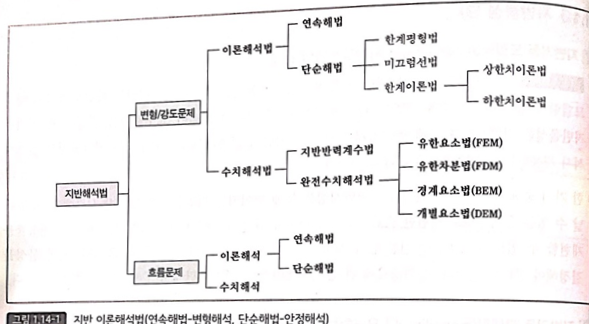
- 수치해석법은 변화하는 지반성상, 다양한 초기조건, 비균질, 이방성, 비선형성 복잡한 경계조건을 가장 사실적으로 고려할 수 있는 해석법
- 적용범위가 가장 넓은 방법
- 목적물에 대한 안정과 변위, 인접구조물의 거동문제에 대한 해를 제공
- 수치해석은 지반재료거동의 수학적모델(구성방정식)에 기초하므로 그 자체로서 결과값을 도출할 수 있음
- 하지만 수학모델은 검증을 통해 정당성이 확보해야 함
- 모델에 대한 정당성이 확인되면 무한에 가까운 조건에 대하여 시뮬레이션이 가능함
■ 수치해석법의 적용성
- 이론해석법에서는 변형문제(연속해법), 안정문제(단순해법)을 다루지만 경계조건이 복잡할 경우 적용이 어렵다.
- 연속해법은 아주 단순한 지반조건에 대한 해를 얻을 수 있는 한계점이 있고
- 단순해법은 비선형 지반특성을 고려할 수 없고 층상지반 적용에 어려운 한계점이 있다.
- 반면, 수치해석은 광범위한 지반특성과 지층의 변화를 고려할 수 있고, 요소화를 통해 다양한 지반재료 특성과 경계조건을 고려할 수 있다.
■ 수치해석의 해석체계
- (전처리) : 메쉬 생성, 구성모델과 입력물성, 초기 및 경계조건
- (본해석) : 선형해석, 비선형해석
- (후해석) : 결과 정리(데이터, 그래프, 등고선, 벡터 등)
■ 모델링 방법에 따른 수치해석법의 구분
- 지반반력계수 모델링법 : 지반의 거동을 스프링의 거동으로 단순화하는 것으로 지반-구조물 상호작용을 조사하기 위해 사용됨
- 완전수치모델링법
- 대상지반문제의 모든 부분을 모델링에 포함한다.
- 특히 실제적인 흙의 응력-변형률 거동과 현장조건과 일치하는 경계조건을 고려할 수 있다.
- 현장조건을 정확하게 반영하는 능력은 흙의 거동을 나타내는 구성방정식의 적정설과 부여한 경계조건의 정확성에 달려있다.
- 연속모델링법 : FEM(유한요소법), FDM(유한차분법)
- 불연속모델링법 : DEM(개별요소법)
- 수리거동과 역학거동의 결합여부에 따른 연계해석과 비 연계해석
- 연계해석 : Terzaghi 유효응력 방정식에 근거하여 전응력을 유효응력과 수압으로 구분하여 수리거동과 역학거동을 같이 연계해서 해석하는 방법, 침투수압에 의한 간극수압을 응력해석에 연속해서 고려하는 해석
※ 연계해석 3가지 사례
* 옹벽의 배수설계 : 침투해석 → 유선망 →간극수압 분포 고려 → 안전율 검토
* 가설흙막이 구조물 굴착저면 안정검토 : 침투해석 → 유선망 → 침투수력 → 안전율 검토
* 불포화토 거동을 고려한 사면안정해석 : 침투해석 → 간극수압 분포고려 → 안전율 검토
- 비연계해석 : 암반역학에서는 유효응력 방정식을 적용할 수 없기 때문에 수리거동과 역학거동을 연계해서 해석하기 어렵다. 따라서, 터널의 수치해석시 지반과 지하수를 따로 분석하고 두 해를 추후에 연합하여 문제를 해결하는 비 연계해석을 주로 이용함
※ 터널설계에서 역학거동과 수리거동을 비 연계해석 사례
* 지반분류(암반분류법 이용) → 표준 지보패턴에 근거한 초기설계 → 초기 설계된 터널단면에 대한 안정해석(응력해석과 변형해석)을 실시
* 터널의 배수형식에 따라(완전배수개념, 침투를 고려한 배수개념, 비배수형 터널) 지하수를 고려한 터널설계 해석(응력해석과 변형해석)을 별도로 실시함


